Introduction
When measuring G2 curvature continuity at the boundary of two surfaces, a result of dev=1.0 is sometimes shown. This was displayed as 'flat' in earlier software versions and only occurs when one of the surfaces is flat in one direction, at the boundary.

Although this is shown as an error, it is in fact an 'exception' in the mathematical formula for calculating G2 deviation, and may not indicate a visual problem. As always with curvature evaluation, use the zebra stripes / iso-angle and the comb plots to double-check the results. In this example, the surfaces are good.
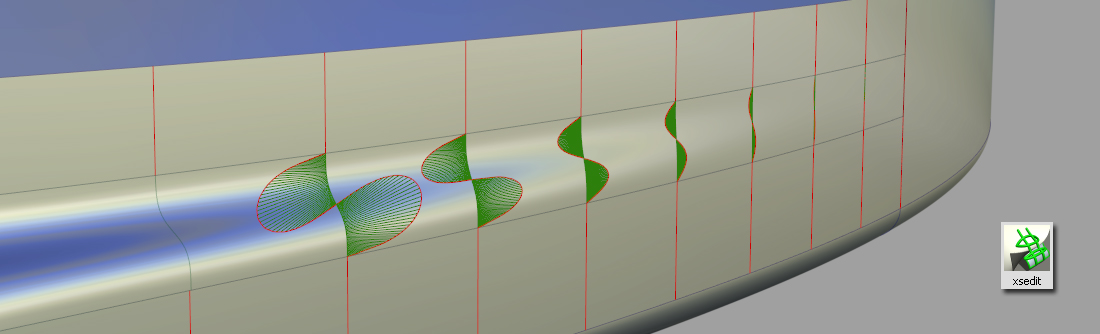

Responding to a dev = 1.0 result
Unless there is some design requirement that means you want to avoid any flat areas, then the result of dev=1.0 can be treated in the same way as any other curvature failure, and other surface checks used to judge the surface quality (iso-angle, zebra stripes, comb plots).
Understanding Continuity with 'Flat' Surfaces
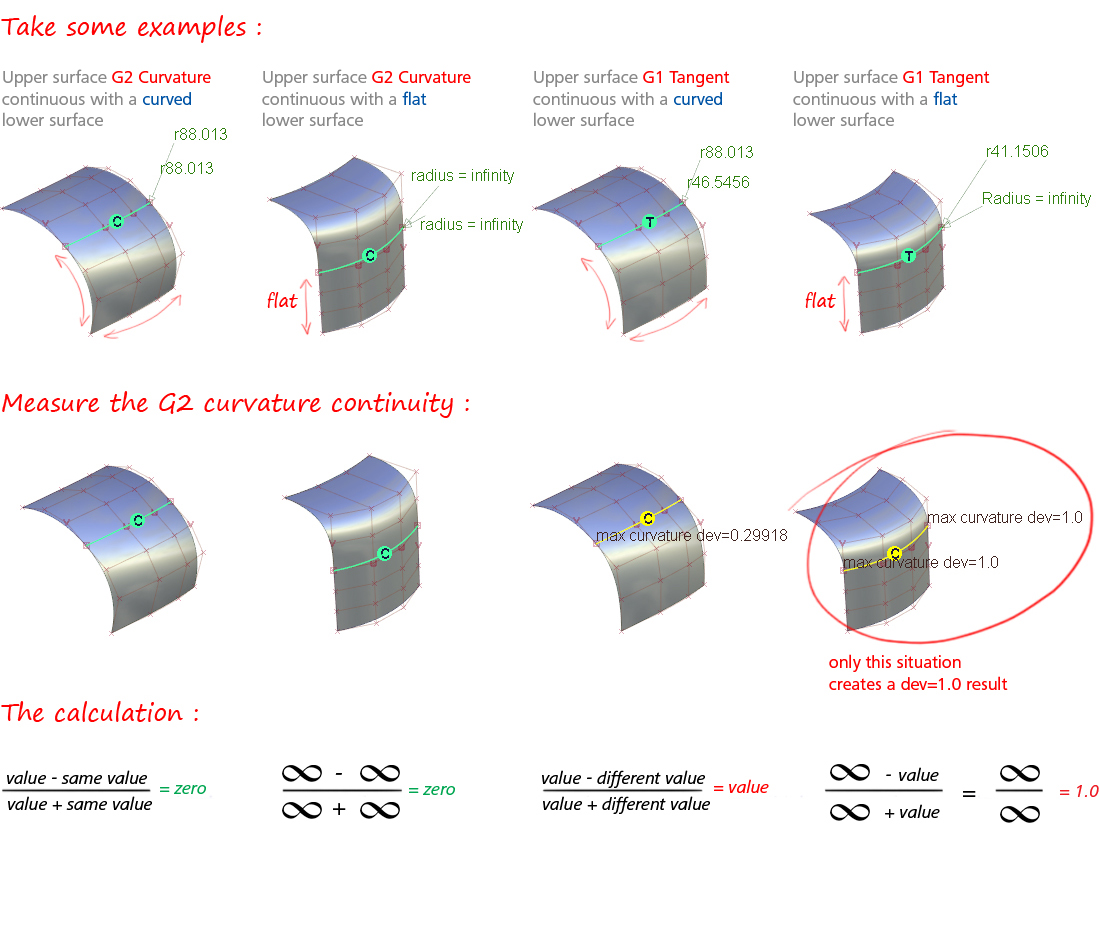
This situation only arises when:
- One of the surfaces is 'flat' (i.e. has a radius of infinity) in the direction in which continuity is being measured (perpendicular to the boundary).
- And G2 Curvature is not achieved, i.e. the matching surface does not have a radius of infinity at the point where they meet.
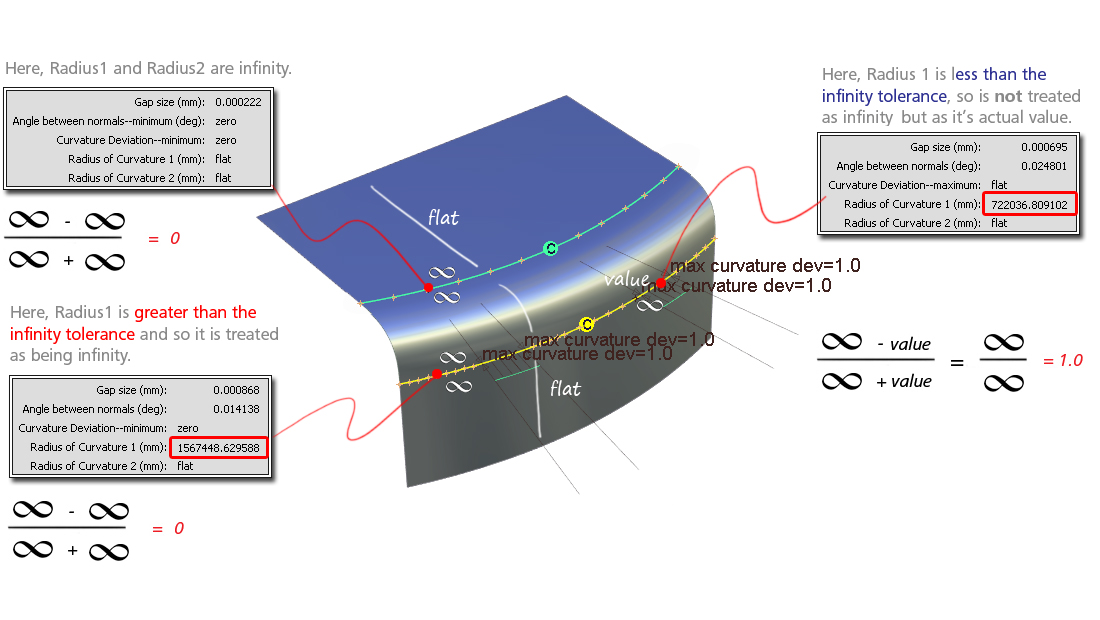
The calculation for G2 Curvature deviation at a boundary is (ignoring negative values): dev = (R1 - R2) / (R1 + R2). The result dev=1.0 is a mathematical exception that can be understood by applying the formula to the surface examples below:
Infinity Tolerance
The software defines any radius greater than 100000 cm as infinity for the purposes of the curvature deviation calculation. Users can modify this value by changing the environment variable : ALIAS_G2_INFINITY_TOL .
In the example below, the two primary surfaces are flat in one direction (perpendicular to the boundary).
Ot the top edge, the fillet has achieved a radius of infinity (flat curvature) at the boundary, so no failure is shown.
On the lower edge, at some checkpoints curvature is calculated as zero, at others dev=1.0. The difference is due to the infinity tolerance of 1,000,000 mm.